Neural Networks

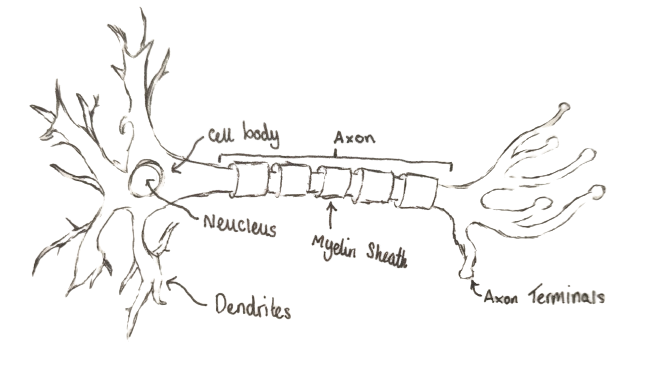
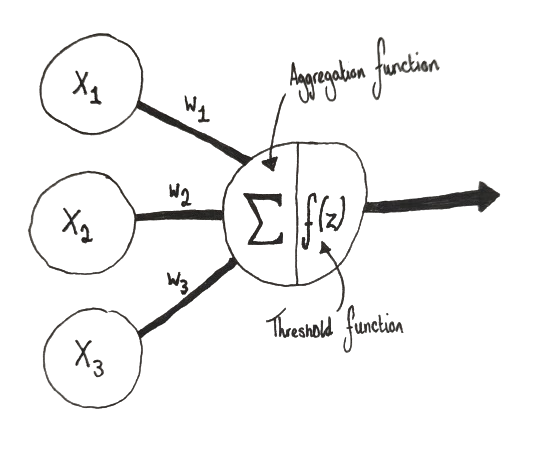
Neuron Diagram

Introduction

Artificial Intelligence is an ever expanding topic of computing more specifically neural networks are a very powerful tool for predictive analysis, but how do they work, and what can they do?

The Neuron and Perceptron

A neural network is a recreation of a animals nervous system within a computer, which attempts to imitate brain functionality. They consist of "Perceptrons" which are inspired by neurons, the role of which is to transmit electrical signals across the animals body both to and from the brain. The Perceptron was first theorized in 1943 by Warren McCulloch and Walter Pitts, followed by the first version built on a computer by Frank Rosenblatt in 1957.

A Perceptron -as introduced by Frank Rosenblatt- was originally intended to be a machine, funded by the US Navy and Air Force simply worked on binary inputs (1s or 0s) that were multiplied by a static weight 0 through 1 (0, 0.1, ..., 1) that was set based on the importance of that input. A real life example of this would be say you want to go to the beach and there is a multitude of factors that affect whether you will actually go e.g. if its sunny, if its low tide or if the beach is quiet. If it's sunny is deemed most important so you would assign it's connection a high weight say 0.7 and if it's a low tide is still important but less so, say 0.5, and if it's quiet gets 0.3 because its least important.

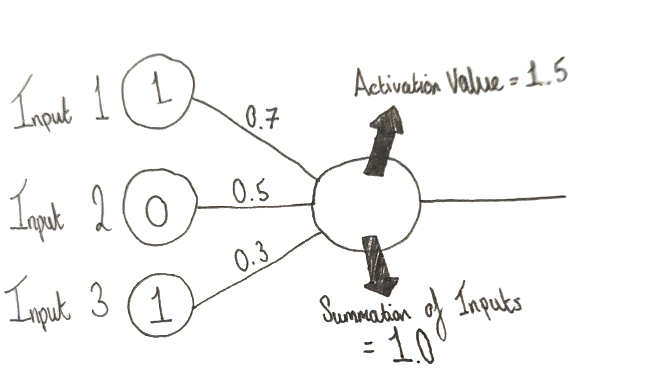
Example Original Perceptron

Each Perceptron would have an activation value/ threshold and if the summation of the inputs multiplied by their respected weights would surpass that number the Perceptron would activate.

However, over time the Perceptron evolved and a representation of that can be seen at the top of this paper in the Perceptron diagram. Firstly, using a Aggregation function summing all inputs multiplied by their weight together then adding a bias this is shown as:

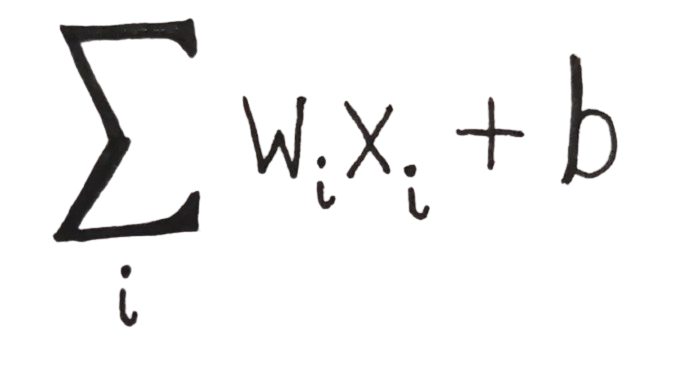
An Aggregation Function

The result of that summation is then passed into an Activation function. This allows the neuron to add non-linearity to the output. There are many different types of activation functions that you can use, ranging from the step function to ReLU, each having their own strengths and weaknesses.

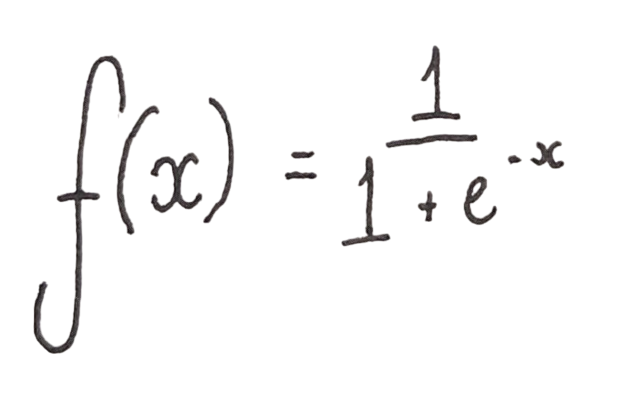
the Sigmoid Logistic Function

using the Sigmoid function as a example we can replace the domain of the function (𝑥) with the output of the aggregation function. e or Euler's number is a irrational number and is the base of Natural Logarithms that is roughly 2.71828182845904..., Adding non linearity allows the Neural Network to model more complex relationships for example:

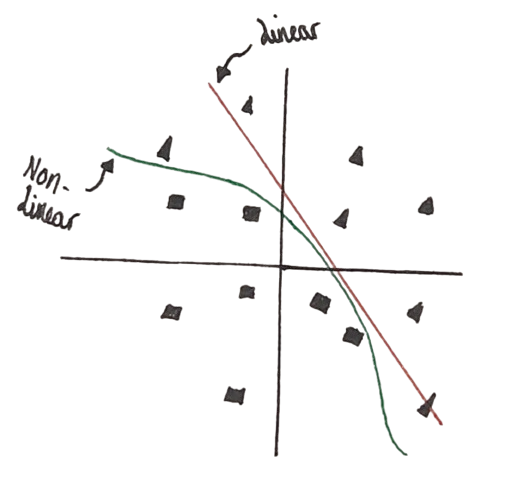
Example decision boundary linear and non-linear(made for example purpose only no real data used )

A decision boundary is a partition that separates vector space into 2 sets, in an ideal world either side of the boundary would only contain a singular class of data. As shown in the Example, non-linearity does a far better job than linear of separating the squares from the triangles.

Perceptron Diagram

Dendrites/ Connections

When connecting Perceptrons together it requires a link in a neuron this would be a dendrodendritic synapse whereas in a Perceptron this goes by a few names such as edges or connections. These hold very minimal information, just the weight of itself (the connection) and which Perceptron it is connected to.

A Neural Network

An individual Perceptron is a Neural Network within itself however In 1958 Frank Rosenblatt introduced a layered network with multiple Perceptrons which can be used to solve much more complex problems, and then depending on the amount of layers they can be classified into shallow neural networks and deep neural networks (typically if they have 2 or more hidden layers ). There is also networks that are not sorted into layers though these are uncommon.

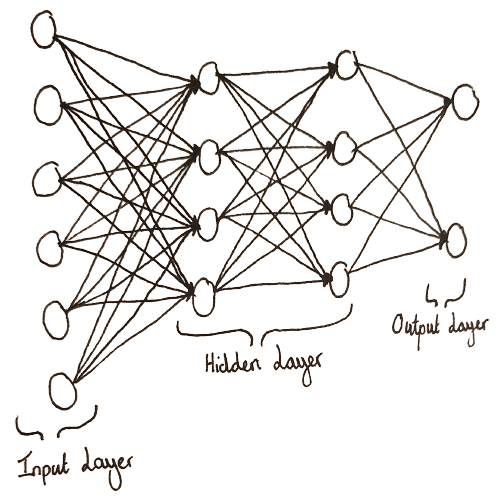
A neural network layout

In a multi-layer Neural Network there are different types of layers, including: The Input Layer, Hidden Layers and the Output Layer and each serve an important, unique purpose within the Net.

Starting at the input Layer this is where the network takes data in, These Perceptrons have no Dendrons (incoming connections also known as incoming edges) and passes on the data into the hidden layers. The Hidden Layers in the network simply compute the input which comes from the previous layer and outputs to the next layer and repeats until it is passed into the Output layer which makes the actual prediction based on its inputs.

Backpropagation

The way multilayer networks adjust the weights across the network is based on the amount of error in the output, now how do you know what weights need to be adjusted and by how much? Backpropagation! first shown off in the 1960s and popularized in 1989 by Rumelhart, Hinton and Williams in their paper “Learning representations by back-propagating errors”. Backpropagation uses a method called the chain rule and to understand the chain rule we first need to understand some notation namely Leibniz notation.

In Leibniz notation d𝑥, d𝑦 is used to represent infinite decrements of 𝑥 and 𝑦. Whereas Δ𝑥 and Δ𝑦 represent finite increments of 𝑥 and 𝑦. ^d𝑦⁄_d𝑥 means the first derivative of 𝑦 with respect to 𝑥.

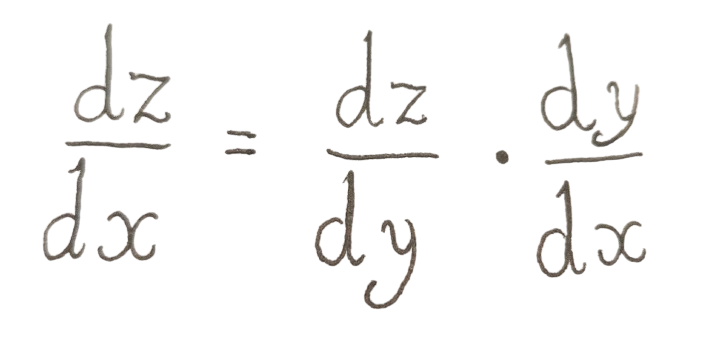
The Chain Rule

Simplified the chain rule is that calculating the instantaneous rate of change of z relative to 𝑦 where 𝑦 is relative to 𝑥 means you can calculate z relative to 𝑥 as the product of two rates of change